Difference between revisions of "Scattered Context Grammars research"
| Line 179: | Line 179: | ||
<math>(A_1, \ldots, A_n) \rightarrow (x_1, \ldots, x_n) \in P</math> | <math>(A_1, \ldots, A_n) \rightarrow (x_1, \ldots, x_n) \in P</math> | ||
| − | satisfies ''x_i ∈ V<sup>+</sup> | + | satisfies ''x_i ∈ V<sup>+</sup>'' for all ''1 ≤ i ≤ n''. The ''propagating scattered context language'' is a language generated by a propagating scattered context grammar. The family of languages generated by propagating scattered context grammars is denoted by |
<math>\mathcal(PSC)</math>. | <math>\mathcal(PSC)</math>. | ||
| Line 194: | Line 194: | ||
The family of languages generated by propagating scattered context grammars which use leftmost or rightmost derivations is denoted by | The family of languages generated by propagating scattered context grammars which use leftmost or rightmost derivations is denoted by | ||
| − | <math>\mathcal(PSC, lm) | + | <math>\mathcal(PSC, lm) \textrm{ or } \mathcal(PSC, rm),</math> |
| + | |||
| + | respectively. To emphasize that the $j$th nonterminal in a sentential form is rewritten during a derivation step in a propagating scattered context grammar $G$ which uses leftmost derivations, we use $\slrRa{^j_{\dleft}}{_G}$ instead of $\slrRa{_{\dleft}}{_G}$. An \index{n-limited derivation@$n$-limited derivation}\emph{$n$-limited derivation}, denoted by $x \lrRa{^n_{\dleft}}{_G^*} y$, is a derivation in which every derivation step $u \lrRa{^j_{\dleft}}{_G} v$ satisfies $j \leq n$. Define the \index{propagating scattered context!language!of degree $n$}\emph{language of degree $n$} generated by $G$ as | ||
\[ | \[ | ||
L(G,\dleft,n) = \{x \in T^* \where S \lrRa{_{\dleft}^n}{^*_G} x\}. | L(G,\dleft,n) = \{x \in T^* \where S \lrRa{_{\dleft}^n}{^*_G} x\}. | ||
Revision as of 16:35, 15 December 2007
!!! WORK IN PROGRESS - Please do not read - and I'm serious about it :-) !!!
Contents
- 1 Introduction
- 2 Basic Definitions
- 3 Results
- 3.1 Known Results
- 3.1.1 Normal Forms of Propagating Scattered Context Grammars
- 3.1.2 Closure Properties of Propagating Scattered Context Grammars
- 3.1.3 Extended Propagating Scattered Context Grammars
- 3.1.4 Propagating Scattered Context Grammars Using Leftmost Derivations
- 3.1.5 Power of Scattered Context Grammars
- 3.1.6 Reduction of Scattered Context Grammars
- 3.2 Own Research
- 3.1 Known Results
- 4 Related Literature
- 5 Contact Information
Introduction
Scattered context grammars were introduced by S. Greibach and J. Hopcroft in 1969 as a straightforward generalization of context-free grammars. Each production of these grammars contains n context-free productions which are applied in parallel to the current sentential form. For example a scattered context production
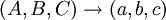
which consists of three context-free productions,
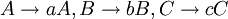 ,
,
is applicable to the sentential form 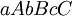 so that all context-free components are applied in parallel and the nonterminals on their left-hand sides are in the same order as they appear in the sentential form. As a result,
so that all context-free components are applied in parallel and the nonterminals on their left-hand sides are in the same order as they appear in the sentential form. As a result,
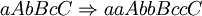 .
.
It is easy to see that by adding productions
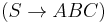
and
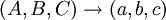 ,
,
where 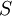 is the start symbol of the grammar, we can easily describe the non-context-free language
is the start symbol of the grammar, we can easily describe the non-context-free language
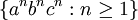 .
.
The first advantage of scattered context grammars can be seen here - by using several context-free productions in parallel, we are able to describe some context-sensitive languages. Furthermore, by only extending context-free grammars, which are well studied and used in many practical applications, we preserve the simplicity of language description. In addition, for modeling context dependencies which span over the whole sentential form (for example in the above example), the description is much simpler than when using ordinary context-sensitive grammars.
Basic Definitions
Formal Languages
The reader is expected to be familiar with the basics of formal language theory. This section is intended to describe the used terminology rather than to explain the basics of formal language theory.
An alphabet V is a finite nonempty set,
whose members are called symbols. The cardinality of V, |V|, is the number of V's members. A finite sequence of symbols from V is a string or, synonymously, a word over V; specifically, 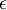 is referred to as the empty string. The
length of a string x ∈ V *, denoted by |x|,
is the number of elements in x. For U ⊆ V, |x|U denotes the number of occurrences of elements from U in a string x.
By
is referred to as the empty string. The
length of a string x ∈ V *, denoted by |x|,
is the number of elements in x. For U ⊆ V, |x|U denotes the number of occurrences of elements from U in a string x.
By  , we denote the set of all strings over V;
, we denote the set of all strings over V; 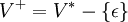 . Any subset L ⊆ V* is a language over V. By
. Any subset L ⊆ V* is a language over V. By 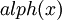 we denote the set of all symbols occurring in a string x. Set
we denote the set of all symbols occurring in a string x. Set
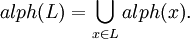
Let x,y ∈ V* be two strings over an alphabet V. The
concatenation of x with y, denoted by xy, is the string
obtained by appending y to x.
For all i ≥ 0 the ith power of x,
denoted by 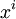 , is recursively defined as
, is recursively defined as
-
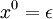 and
and -
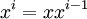 for i ≥ 1.
for i ≥ 1.
The reversal of x, denoted by 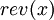 , is x written in the reverse order. Let L1, L2 ⊆ V* be
two languages over V. The concatenation of
, is x written in the reverse order. Let L1, L2 ⊆ V* be
two languages over V. The concatenation of 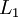 and
and 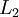 , denoted by L1L2, is defined as
, denoted by L1L2, is defined as
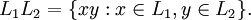
The right quotient of 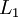 with respect to
with respect to 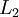 , denoted by
, denoted by 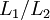 , is defined as
, is defined as
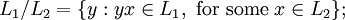
similarly, the left quotient of 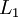 with respect to
with respect to 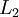 , denoted by L2 \ L1, is defined as
, denoted by L2 \ L1, is defined as
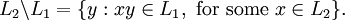
We also use a special type of the right and the left quotient. The exhaustive right quotient of 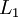 with respect to
with respect to 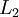 , denoted by
, denoted by 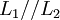 , is defined as
, is defined as
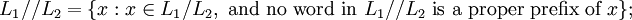
similarly, the exhaustive left quotient of 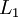 with respect to
with respect to 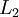 , denoted by L2 \\ L1, is defined as
, denoted by L2 \\ L1, is defined as
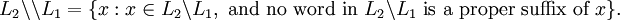
Apart from binary operations, we also make some unary operations with languages. Let L ⊆ T*. The ith power of L, Li, is defined as
- L0 = {ε} and
- Li = L Li-1 for i ≥ 1.
The Kleene star of L, L*, is defined as
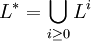
and the Kleene plus of L, L+, is defined as
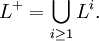
Notice that L+ = L L* = L* L and L* = L+ ∪ {ε}.
References
(pdf) A. Meduna. Automata and Languages: Theory and Applications. Springer, 2000, pp. 920.
(pdf) G. Rozenberg and A. Salomaa. Handbook of Formal Languages. Springer, 1997, pp. 2051.
(pdf) A. Salomaa. Formal Languages. Academic Press, 1973, pp. 322.
Scattered Context Grammars
A scattered context grammar is a quadruple
G = (V, T, P, S),
where
- V is the total alphabet,
- T ⊂ V is the set of terminals,
- P is a finite set of productions of the form
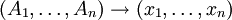 , where n ≥ 1, Ai ∈ V-T and xi ∈ V* for all 1 ≤ i ≤ n,
, where n ≥ 1, Ai ∈ V-T and xi ∈ V* for all 1 ≤ i ≤ n, - S ∈ V - T is the start symbol of G.
If Failed to parse (unknown error): \begin{array}{r@{\;}l} u & = u_1 A_1 u_2 A_2 \ldots u_n A_n u_{n+1}, \\ v & = u_1 x_1 u_2 x_2 \ldots u_n x_n u_{n+1}, \end{array}
and
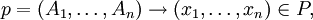
where ui ∈ V* for all 1 ≤ i ≤ n, then G makes a derivation step from u to v according to p, symbolically written as
![u \Rightarrow_G v \; [p],](/en/images/math/8/4/d/84d1659d135c2e1ec4d3d15e5977c4f0.png)
or, simply, u ⇒ G v. In addition, if Ai ∉ alph(ui) for all 1 ≤ i ≤ n, then the direct derivation is leftmost, and we write
![u {}_{lm}\Rightarrow_G v \; [p];](/en/images/math/4/1/0/410050f6aa29ec4eb26b3f08c4d6c176.png)
if Ai ∉ alph(ui+1) for all 1 ≤ i ≤ n, then the direct derivation is rightmost, and we write
![u {}_{rm}\Rightarrow_G v \; [p].](/en/images/math/c/1/0/c100cf7ef8f53e0b91da9e277cb5e43e.png)
Set
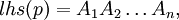
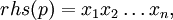
and
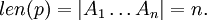
If len(p) ≥ 2, p is said to be a context-sensitive production, while for len(p) = 1, p is said to be context-free. The scattered context language, is a language generated by a scattered context grammar G = (V, T, P, S), denoted by L(G), and defined as

If every derivation step in every successful derivation in G is leftmost, G generates L(G) in a leftmost way. If every step in every successful derivation in G is rightmost, G generates L(G) in a rightmost way. The family of languages generated by scattered context grammars is denoted by
 .
.
A propagating scattered context grammar is a scattered context grammar 'G = (V, T, P, S)' in which each
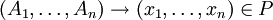
satisfies x_i ∈ V+ for all 1 ≤ i ≤ n. The propagating scattered context language is a language generated by a propagating scattered context grammar. The family of languages generated by propagating scattered context grammars is denoted by
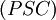 .
.
A propagating scattered context grammar which uses leftmost or rightmost derivations is a propagating scattered context grammar G = (V, T, P, S) whose language is defined as
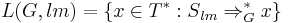
or
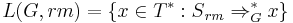
respectively. The family of languages generated by propagating scattered context grammars which use leftmost or rightmost derivations is denoted by
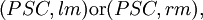
respectively. To emphasize that the $j$th nonterminal in a sentential form is rewritten during a derivation step in a propagating scattered context grammar $G$ which uses leftmost derivations, we use $\slrRa{^j_{\dleft}}{_G}$ instead of $\slrRa{_{\dleft}}{_G}$. An \index{n-limited derivation@$n$-limited derivation}\emph{$n$-limited derivation}, denoted by $x \lrRa{^n_{\dleft}}{_G^*} y$, is a derivation in which every derivation step $u \lrRa{^j_{\dleft}}{_G} v$ satisfies $j \leq n$. Define the \index{propagating scattered context!language!of degree $n$}\emph{language of degree $n$} generated by $G$ as \[
L(G,\dleft,n) = \{x \in T^* \where S \lrRa{_{\dleft}^n}{^*_G} x\}.
\] If $L(G, \dleft, n) \neq L(G, \dleft)$ for all $n \geq 1$, then $L(G, \dleft)$ is said to be of \index{propagating scattered context!language!of infinite degree}\emph{infinite degree}. The family of languages of degree $n$ generated by propagateing scattered context grammars which use leftmost derivations is denoted by $\lfam{\PSC, \dleft, n}$, and $\lfam{\PSC, \dleft, \infty} = \bigcup_{n=1}^{\infty}\lfam{\PSC, \dleft, n}$.
References
(pdf) S. Greibach, J. Hopcroft. Scattered Context Grammars. Journal of Computer and System Sciences, 1969, pp. 233-247.
Results
Known Results
Normal Forms of Propagating Scattered Context Grammars
Based on
(pdf) S. Greibach, J. Hopcroft. Scattered Context Grammars. Journal of Computer and System Sciences, 1969, pp. 233-247.
Closure Properties of Propagating Scattered Context Grammars
Based on
(pdf) S. Greibach, J. Hopcroft. Scattered Context Grammars. Journal of Computer and System Sciences, 1969, pp. 233-247.
Extended Propagating Scattered Context Grammars
Based on
(pdf) J. Gonczarowski, M. K. Warmuth. Scattered Versus Context-Sensitive Rewriting. Acta Informatica, 1989, pp. 81-95.
Propagating Scattered Context Grammars Using Leftmost Derivations
Based on
(pdf) V. Virkkunen. On Scattered Context Grammars. Acta Universitatis Ouluensis, 1973, pp. 75-82.
Power of Scattered Context Grammars
Based on
(pdf) V. Virkkunen. On Scattered Context Grammars. Acta Universitatis Ouluensis, 1973, pp. 75-82.
Reduction of Scattered Context Grammars
Based on
(pdf) A. Meduna. Economical Transformations of Scattered Context Grammars to Phrase-Structure Grammars. Acta Cybernetica, 1998, pp. 225-242.
(pdf) A. Meduna. Generative Power of Three-Nonterminal Scattered Context Grammars. Theoretical Computer Science, 2000, pp. 625-631.
(pdf) G. Vaszil. On the Descriptional Complexity of Some Rewriting Mechanisms Regulated by Context Conditions. Theoretical Computer Science, 2005, pp. 361-373.
Own Research
Generation of Sentences with Their Parses
Based on
(pdf) A. Meduna, J. Techet. Generation of Sentences with Their Parses: the Case of Propagating Scattered Context Grammars. Acta Cybernetica, 2005, pp. 11-20.
(pdf) A. Meduna, J. Techet. Canonical Scattered Context Generators of Sentences with Their Parses (to appear). Theoretical Computer Science, 2007/8, pp. ???-???.
(pdf) J. Techet. Scattered Context Generators of Sentences with Their Parses. Pre-proceedings of the 1st Doctoral Workshop on Mathematical and Engineering Methods in Computer Science, 2005, pp. 68-77.
(pdf) A. Meduna, J. Techet. Reduction of Scattered Context Generators of Sentences Preceded by Their Leftmost Parses. Proceedings of 9th International Workshop on Descriptional Complexity of Formal Systems, 2007, pp. 178-185.
References
(pdf) V. Geffert. Context-Free-Like Forms for the Phrase-Structure Grammars. Proceedings of the Mathematical Foundations of Computer Science 1988, 1988, pp. 309-317.
(pdf) H. C. M. Kleijn and G. Rozenberg. On the Generative Power of Regular Pattern Grammars. Acta Informatica, 1983, pp. 391-411.
k-Limited Erasing
Based on
(pdf) J. Techet. k-Limited Erasing Performed by Scattered Context Grammars. Proceedings of the 2nd International Workshop on Formal Models WFM '07, 2007, pp. 227-234.
Scattered Context Grammars with Non-Context-Free Components
Based on
(pdf) J. Techet. A Note on Scattered Context Grammars with Non-Context-Free Components. MEMICS 2007 Proceedings, 2007, pp. 225-232.
References
(pdf) O. Ibarra. Simple Matrix Languages. Information and Control, 1970, pp. 359-394.
(pdf) G. Paun. Linear Simple Matrix Languages. Elektronische Informationsverarbeitung und Kybernetik, 1978, pp. 377-384.
Maximal and Minimal Rewriting
Based on
(pdf) A. Meduna, J. Techet. Maximal and Minimal Scattered Context Rewriting. FCT 2007 Proceedings, 2007, pp. 412-423.
References
(pdf) Takumi Kasai. An Hierarchy Between Context-Free and Context-Sensitive Languages. Journal of Computer and System Sciences, 1970, pp. 492-508.
n-Limited Derivations
References
(pdf) Takumi Kasai. An Hierarchy Between Context-Free and Context-Sensitive Languages. Journal of Computer and System Sciences, 1970, pp. 492-508.
Related Literature
(pdf) Armin B. Cremers. Normal Forms for Context-Sensitive Grammars. Acta Informatica, 1973, pp. 59-73.
(pdf) H. Fernau. Scattered Context Grammars with Regulation. Annals of Bucharest University, Mathematics-Informatics Series, 1996, pp. 41-49.
(pdf) D. Milgram, A Rosenfeld. A Note on Scattered Context Grammars. Information Processing Letters, 1971, pp. 47-50.
(pdf) J. Techet. Částečně paralelní generování jazyků. Faculty of Information Technology BUT, 2005, pp. 55.
Contact Information
- Address: Jiří Techet, Faculty of Information Technology, Brno University of Technology, Božetěchova 2, Brno 61266, Czech Republic
- Email: techet@fit.vutbr.cz
- Web Page: www.fit.vutbr.cz/~techet
Jiri 11:06, 26 November 2007 (CET)